Numeros Complejos

Números complejos


 
Podemos esquematizar los conjuntos numéricos de la siguiente manera:


Recordar:
que cualquier número elevado al cuadrado o con potencia par siempre dará un numero positivo.
-22 = 4                   -82 = 64                 -24 = 16

Siendo la radicación la inversa de la potenciación es imposible obtener la raíz cuadrada de un numero negativo.

Aclarar que esto solo se cumple en radicales con índices pares, ya que cuando es impar es posible obtener un resultado.


 ¿Cómo surgen los números imaginarios?
Surgen con la necesidad de hacer verdaderas las siguientes igualdades: x2 + 1 = 0, x2 + 4 = 0


Por definición  es la unidad imaginaria, que se simboliza por i y cualquier numero imaginario es un múltiplo de i como:

Número Imaginario (bi)
Es un número real b acompañado de la unidad imaginaria i (bi).

Ejemplos


Numero complejo en forma binómica o aritmética
La expresión a + bi es un numero complejo, donde a y b son números reales e i la unidad imaginaria; a es la componente real y bi es la componente imaginaria.

Forma canónica o de par ordenado de un numero complejo
Cuando expresamos el numero complejo de forma (a, b) constituye la forma canónica o par ordenado.

Complejos iguales
Dos números complejos (a, b) y (c, d) son iguales si y solo si a = c y b = d.

Real puro
Es un numero complejo cuya componente imaginaria es cero: a + bi. También la expresamos (a, 0).

Ejemplos:
                               3 + 0i = 3              y             -2 + 0i = -2

Imaginario puro
Es un numero complejo cuya componente real es cero: 0 + bi. También se expresa (0, b).

Ejemplos:
                             

Representación gráfica de los números complejos
Los números complejos se representan en el plano guassiano.

Ejemplo:
Representar los siguientes números complejos: -4 – 3i y 4 + 2i


Complejos opuestos
Son aquellos que difieren en el signo sus primeras y segundas componentes respectivamente.

Ejemplo:
                               El complejo opuesto de      -3 + 4i           es           3 – 4i
Representar gráficamente los complejos opuestos anteriores.

Compuestos conjugados
Son aquellos que difieren únicamente en el signo de sus componentes imaginarias.

Ejemplo:
                               4 + 2i     su conjugado es              4 – 2i
Representar gráficamente los complejos conjugados anteriores.

Potencias de i
i0 = 1
i = , por definición.
i2 = -1
i3 = i2 x i = (-1) (i) = -i
i4 = i2 x i2 = (-1) (-1) = 1

Ejercicios

Halle las siguientes potencias de i:
i5 =
i6 =
i2 =
i0 =

Operaciones en los números complejos expresados en forma binómica


Adición de dos números complejos
Dados dos números complejos (a + bi) y (c + di) la suma es igual a (a + c) + (b + d)i

Ejemplo:
                  (4 – 2i) + (6 + 8i) = (4 + 6) + (-2 + 8)i = 10 + 6i

Sustracción
Para obtener este complejo procedemos a cambiar los signos al complejo sustraendo y sumarlo al complejo minuendo.

Ejemplo:
                   (6 + 3i) – (2 – i) = (6 – 2) + (3 + 1)i = 4 + 4i

Ejercicios:
  • Comprobar que la suma de dos complejos opuesto es cero:

(2 – 3i) + (-2 + 3i)

  • Comprobar que la suma de dos complejos conjugados es un real puro:

(4 – 2i) + (4 + 2i)

Resuelva:
  1. (3 + 2i) + (5 + 3i)
  2. (7 - 10i) – (9 + 4i)
  3. (4 + 7i) + (9 – 4i)
  4. (20 – 5i) – (14 + 13)

Multiplicación

Esta dada por: (a + bi) x (c + di) = ac + adi + bic +bidi = ac + adi + bci + bdi2 = ac + adi + bci + bd(-1) = ac + (ad + bc)i – bd = (ac – bd) + (ad + bc)i

Es similar al procedimiento que utilizamos para multiplicar dos binomios algebraicos.

Ejemplo:
                Multiplicar (3 – 2i) (5 + i) = 15 + 3i – 10i – 2i2 = 15 – 7i – 2(-1) = 15 – 7i + 2 = 17 – 7i

Ejercicios

Multiplique:
  1. (3 – 2i)(2 + i)
  2.  (8 – 5i)(4 – 3i)
  3.  (-6 + i)(4 - 6)
  4. (-10 + 5i)(1 – i) 

División de números complejos

Para dividir dos números complejos multiplicamos el dividendo y el divisor por el complejo conjugado del divisor de la expresión dada, y después proceder a efectuar las operaciones. El resultado final será un complejo en la forma binómica a + bi.

Ejemplo:


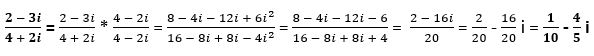
Comentarios

Publicar un comentario

Entradas más populares de este blog

Trigonometría Plana

Imagen
Trigonometría Plana ¿Qué es la trigonometría? Es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. Estudia las relaciones entre los lados y los ángulos de triángulos, de las propiedades y aplicaciones de las funciones trigonométricas de ángulos. ¿Qué es la trigonometría plana? La trigonometría plana se ocupa del estudio de las figuras contenidas en un plano. ¿Qué es la trigonometría esférica? La trigonometría esférica se ocupa del estudio de los triángulos que forman parte de la superficie de una esfera. Lados de un triángulo rectángulo La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo. El cateto opuesto es el lado opuesto al ángulo. El cateto adyacente es el lado adyacente al ángulo. A : es el ángulo A B : es el ángulo B C : es el ángulo recto de 90 0 b = cateto opuesto del ángulo B a = cateto adyacente del ángulo B h = Hipotenusa La su...
Leer más

Análisis Combinatorio

Imagen
Análisis Combinatorio ·          El análisis combinatorio estudia las características de las distintas formaciones que podemos hacer con un finito de m elementos dados. Teorema fundamental del análisis combinatorio Si un evento ocurre P maneras diferentes un segundo de T maneras diferentes y asi sucesivamente… Z eventos independientes entre si cada uno del otro, todos estos eventos en el mismo orden ocurrirán de P*T*…*Z maneras diferentes. Ejemplo: Para ir a Santo Domingo a Santiago hay 3 maneras: carro, avión y guagua. Para ir de Santiago a puerto plata hay 2 maneras: guagua y tren. ¿De cuantas maneras puede ir un ciudadano de Santo Domingo a Puerto Plata, pasando por Santiago? Tenemos 3 maneras de S.D. a Stgo., que sería P maneras y 2 maneras de Stgo. a Puerto Plata, que sería T maneras. P x T = 3 x 2 = 6 maneras. Ejercicios 1. Con los dígitos del 1 al 9. ¿Cuántos números de tres cifras no necesariamente d...
Leer más

Conjuntos Numéricos

Imagen
Conjunto de los números naturales El conjunto de los números naturales es el primer conjunto y surge de manera empírica para satisfacer la necesidad de cuantificar. Este conjunto permite contar y ordenar. Se representa con la letra N y se expresa así: N = (1,2,3,4...) ó N = (1,2,3,4..., n + 1, n + 2,...) Propiedades del conjunto de los números naturales: El conjunto de los números naturales es ordenable.  El conjunto de los números naturales tiene un primer elemento y no tiene un último elemento, es decir, es un conjunto infinito.  Entre dos números naturales consecutivos no existe ningún otro número natural.  Todo número natural n posee un número natural anterior,  menos el 1. Esto implica que el 1 es el primer número natural.  A todo número natural sigue otro número natural . Conjunto de los números enteros Este conjunto surge de la necesidad de ampliar el conjunto de los números naturales. El hombre tiene la necesidad de expresa...
Leer más