Trigonometría Plana
Trigonometría Plana
¿Qué es la
trigonometría?
Es una rama de la matemática, cuyo significado etimológico
es 'la medición de los triángulos'. Estudia las relaciones entre los lados y
los ángulos de triángulos, de las propiedades y aplicaciones de las funciones
trigonométricas de ángulos.
¿Qué es la
trigonometría plana?
La trigonometría plana se ocupa del estudio de las figuras
contenidas en un plano.
¿Qué es la
trigonometría esférica?
La trigonometría esférica se ocupa del estudio de los triángulos
que forman parte de la superficie de una esfera.
Lados de un triángulo
rectángulo
- La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
- El cateto opuesto es el lado opuesto al ángulo.
- El cateto adyacente es el lado adyacente al ángulo.
A: es el ángulo A
B: es el ángulo B
C: es el ángulo
recto de 900
b = cateto opuesto del ángulo B
a = cateto adyacente del ángulo B
h = Hipotenusa
La suma de los ángulos
A + B + C = 1800
Completa usando
el triángulo anterior
Es el cateto opuesto del ángulo A _______
Es el cateto adyacente del ángulo A ________
Funciones Trigonométricas
Ejemplo:
Ejercicio
Usando el triángulo rectángulo anterior calcular las
funciones trigonométricas con respecto al ángulo A.
Teorema de Pitágoras
El cuadrado de la hipotenusa de un triángulo rectángulo es
igual a la suma de los cuadrados de los catetos.
Ejemplo:
Calcular la
hipotenusa del triángulo rectángulo siguiente:
Ejercicios
Halle por el
teorema de Pitágoras las distancias que faltan en los siguientes triángulos rectángulos:
Calculo de las
funciones trigonométricas
Funciones trigonométricas
de 450
Funciones
trigonométricas de 300 y 600
Funciones de ángulos cuadrantes
Consideramos el triángulo rectángulo ABD en cada uno de los cuadrantes del
sistema de ejes cartesiano.
Calcular Funciones trigonométricas de:
Funciones trigonométricas en los ejes
Funciones
trigonométricas de 00
…
Funciones
trigonométricas de 1800
…
Funciones
trigonométricas de 2700
…
Funciones
trigonométricas en el segundo cuadrante
Funciones
de 900 + 450 = 1350
…
Funciones
de 900 + 600 = 1500
…
Con
los datos obtenidos llenar la siguiente tabla:
Identidades trigonométricas
Identidades:
son igualdades que se verifican para cualquier
valor de la variable o variables que participan en la igualdad.
Funciones trigonométricas de la suma de dos ángulos
Para poder hallar las funciones
trigonométricas de la suma de dos ángulos utilizaremos las siguientes fórmulas
para las tres primeras funciones y para las demás solo aplicaremos la inversa
de estas:
Ejemplo:
Halle
los valores de las funciones trigonométricas de 750
·
Utilizaremos los ángulos
450 + 300 = 750, ya que la suma de estos es 750.
·
Usamos la tabla
anterior de ángulos cuadrantes para conocer los valores de las funciones a
sumar.
·
Las funciones
siguientes son inversas de las anteriores
Ejercicio
Halle los valores de las funciones trigonométricas
de 1350 utilizando la suma de dos ángulos.
Funciones trigonométricas de la diferencia de dos ángulos
Para poder hallar las funciones
trigonométricas de la diferencia de dos ángulos utilizaremos las siguientes
fórmulas para las tres primeras funciones y para las demás solo aplicaremos la
inversa de estas, es bueno notar que estas son las mismas fórmulas para la suma
con la excepción de que los signos son diferentes:
Ejemplo:
Halle
los valores de las funciones trigonométricas de 150
·
Usamos la tabla
anterior de ángulos cuadrantes para conocer los valores de las funciones a
restar.
Ejercicio
Halle los valores de las demás funciones trigonométricas.
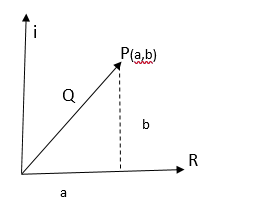
Números complejos en forma polar y trigonométrica
Para
obtener la forma polar y trigonométrica es necesario determinar un módulo o
distancia y un argumento o ángulo.
El módulo de un complejo (Q)
Es
la distancia del origen de coordenadas al punto que representa el conjunto.
Argumento de un complejo (α)
Es el ángulo
formado por el modulo y el eje x en el sentido positivo (ángulo positivo).
Forma polar
Q α
Forma trigonométrica
(a + bi) = Q cos α + Qi sen α =
Q (cos α + i sen α)



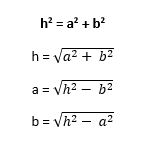






















Comentarios
Publicar un comentario